相似三角形的性质和应用

相似三角形的性质和应用

相似三角形的性质

相似三角形是几何中重要的证明模型之一，它是全等三角形的推广。全等三角形可以被理解为相似比为1的相似三角形。相似三角形的性质主要包括：

1.对应角相等：相似三角形的对应角相等，这是相似三角形最基本的性质之一。

2.对应边成比例：相似三角形的对应边成比例，这也是相似三角形名称的由来。

3.面积比等于相似比的平方：相似三角形的面积比等于相似比的平方。这是由于相似三角形的面积等于对应边长的平方乘以相似比的平方。

4.对应线段的比等于相似比：相似三角形的一切对应线段（对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比。

5.周长比等于相似比：相似三角形周长的比等于相似比。

6.内切圆、外接圆直径比和周长比都和相似比相同，内切圆、外接圆面积比是相似比的平方：这是相似三角形的进一步性质。

相似三角形的判定

相似三角形的判定定理主要有：

1.AA（两角对应相等）：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。

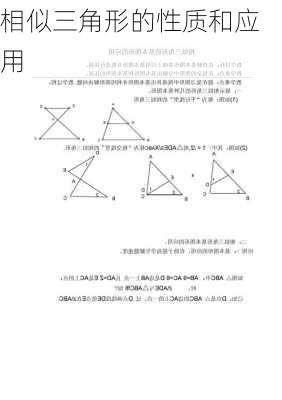
2.SAS（两边成比例且夹角相等）：如果两个三角形的两组对应边成比例，并且对应的夹角相等，那么这两个三角形相似。

3.SSS（三边成比例）：如果两个三角形的三组对应边成比例，那么这两个三角形相似。

4.HL（一条直角边与斜边成比例的两个直角三角形）：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。

5.三边对应平行的两个三角形相似：这是一个推论，来源于上述判定定理。

相似三角形的应用

相似三角形在实际生活中应用广泛，例如：

1.测量物体的高度或长度：通过构造相似三角形，可以利用已知的距离来测量不可直接到达的物体的高度或长度。

2.测量河宽或建筑物的高度：类似的，可以通过构造相似三角形来测量河的宽度或建筑物的高度。

3.解决实际问题中的比例问题：在实际问题中，线段成某个比例的已知条件往往会和三角形相似结合起来，因为三角形相似就能利用线段的比例。

相似三角形不仅是理论上的概念，更是解决实际问题的重要工具。通过理解和掌握相似三角形的性质和判定，可以在各种实际情况下应用这种知识，从而解决各种几何问题。