分块策略在电路中的应用

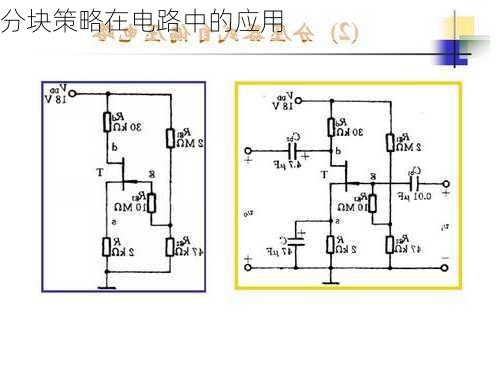
分块策略在电路中的应用

分块策略在电路中的应用广泛，可以从以下几个方面进行阐述：

1.电路分块诊断方法

基于模型的诊断问题在人工智能领域内一直备受关注，将诊断问题转换成SAT（Satisfiable）问题成为解决基于模型诊断问题的一个重要方法。基于目前高效诊断方法LLBRSTree（LastLevelBasedonReverseSearchTree）的研究，提出电路分块诊断方法ACDIAG（AbstractCircuitDiagnosis）方法，对电路进行分块来缩减电路规模，利用LLBRSTree方法对分块后抽象电路求得极小块诊断解；提出诊断解拓展方法，结合分块后电路结构特征对每个极小块诊断解进行直接扩展得到极小诊断解，避免对抽象电路还原后才能得到所有解的问题。

2.电路分块算法

随着集成电路工艺和规模的飞速发展，使得VLSI测试变得日益困难，因此测试技术成为VLSI领域的一个重要研究课题。在分析VLSI测试的瓶颈问题基础上，介绍了几种电路分块算法，分析了分块算法对于VLSI测试的必要性。利用分块算法将原始电路划分为若干子块有利于采用不同BIST结构对子块进行测试，使得一定时间内电路翻转次数降低，而功耗也随之降低；通过比较并行BIST和扫描BIST的实验结果，发现并行BIST获得的系统故障覆盖率高于扫描BIST。

3.分块策略在矩阵乘法中的应用

在许多应用领域中，大规模浮点矩阵乘法往往是最耗时的计算核心之一。在新兴的应用中经常存在至少有一个维度很小的大规模矩阵，我们把具备这种特性的矩阵称为非均匀矩阵。由于FPGA上用以存储中间结果的片上存储器容量十分有限，计算大规模矩阵乘法时往往需要将矩阵划分成细粒度的子块计算任务。当加速非均匀矩阵乘法时，由于只支持固定分块大小，大多数现有的线性阵列结构的硬件矩阵乘法器将遭受很大的性能下降。为了解决这个问题，提出了一种有效的优化分块策略。通过集成224个处理单元，该矩阵乘法器在150MHz的时钟频率下对于实际应用中的非均匀矩乘达到了48GFLOPS的实测性能，而所需带宽仅为4.8GB/s。

4.分块策略在图像处理中的应用

在图像处理中，分块策略也被广泛应用。例如，提出一种基于双线性模板和分块策略的可见光虹膜色素斑检测方法，首先使用两个不同长度的线性模板来检测虹膜色素斑，然后对图像按行列等进行分块，对每个子区域进行检测，提高了检测的准确性和效率。

总的来说，分块策略在电路设计和测试、图像处理、算法设计等多个领域都有广泛的应用，是现代电路设计和计算中不可或缺的一部分。