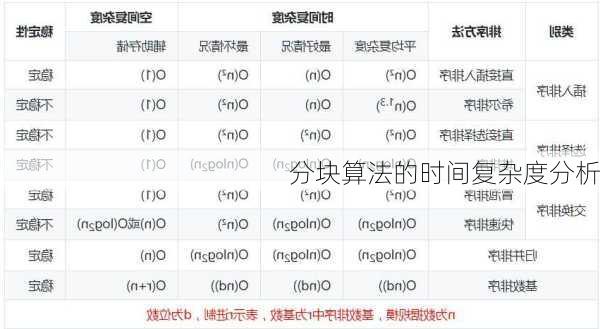
分块算法的时间复杂度通常可以表示为
O(√n),其中
n
是整个数据集的元素数量。这种时间复杂度是基于分块算法的工作原理的,该算法首先通过二分查找或顺序查找在索引表中定位到正确的块,这一步的时间复杂度可以是
O(log
m),其中
m
是索引表的大小。一旦确定了正确的块,就在该块中进行顺序查找,这一步的时间复杂度为
O(k),其中
k
是块的大小。
在实际应用中,分块算法的时间复杂度还会受到其他因素的影响,例如索引项的组织方式、块的大小和分布、以及数据的初始状态等。例如,如果索引项是按照某种高效的数据结构(如哈希表)来组织的,那么查找索引表的时间复杂度可以接近
O(1)。同样,如果块的大小选择得当,可以减少块内查找的时间复杂度。
总的来说,分块算法的时间复杂度分析需要综合考虑索引表的查找时间复杂度和块内查找的时间复杂度,最终结果通常为
O(√n)。然而,在具体的应用场景下,实际的时间复杂度可能会有所不同,取决于上述各种因素。